I’ve mentioned over and over and over again that I’m not a programmer, but a econometrician. Today we put that to good use.
1. The problem
I can think of two ways of producing the list of divisors of a number:
divisors x = [ y | y<-[1..x], (gcd x y) == y]
fdivisors x = [ y | y<-[1..x], x `mod` y == 0]
Intuition would tell us the second one is faster, but is that really a fact?
2. Generating data
To test that, we devise two tests:
test1p n = (n, sum $ map (length . divisors) [1..n])
test2p n = (n, sum $ map (length . fdivisors) [1..n])
Now in good old GNU R, I produce a list of random numbers between 50 and 10000 and paste them over my code.
testdata = [3476,1856,3234,1080,369,2951,4930,4820,2270,2023,4613,3345,2252,2100,1187,643,3657,1493,4043,2439,4706,4885,2328,4294,4923,4427,4892,4147,4134,1215,586]
Now I’m going to engage in some code generation.
produce = putStrLn $ concat $ map wrap testdata where
wrap n = "test1p "++show n ++ "\ntest2p "++show n ++ "\n"
I run produce in GHCi and paste the results on a text file. Next I add the following two lines to the beginning of said file:
:l trigs.hs
:set +s
where trigs.hs is the name of my Haskell code file. We save everything to produce.raw and on a shell window, I type
ghci < produce.raw
This will produce a few dozens of lines like
*Trigs> (3657,30578)
(33.58 secs, 565482232 bytes)
*Trigs> (1493,11140)
(8.95 secs, 291860752 bytes)
*Trigs> (1493,11140)
(5.60 secs, 94533060 bytes)
After everything is said and done, a couple of regexes turns the results into CSV format. We add a line in the beginning naming the columns and switch back into GNU R.
3. Loading and plotting data
This line of R code will load our data into the system:
data<-read.table("~/repos/comparealgos.csv", header=TRUE, sep=",")
Let’s take some plots.
plot(n, time)

plot(n,bytes)

The intuitive story of (a) running time depending on the size of n and (b) the `mod` algorithm being faster than the gcd one seems to hold. But let’s put numbers into this.
4. Linear regression analysis
In a nutshell, linear regresion analysis is about fitting data to an equation (possibly a system of multiple equations in more sophisticated models) and performing statistical tests of whether the fit means anything. The first model we’re going try to fit is the following:
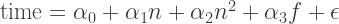
where  is 0 for the gcd algorith and 1 for the mod algorithm, and
is 0 for the gcd algorith and 1 for the mod algorithm, and  accounts for serendipity.
accounts for serendipity.
Note the quadratic term: with this single term, we can both screen for more-than-linear and less-than-linear growth of time on n. Another way to look at this is to differentiate:
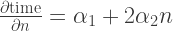
As we see, 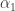 is a constant effect of scale, while
is a constant effect of scale, while 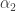 is an effect that varies on the size of n. If
is an effect that varies on the size of n. If 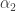 is negative, we have a smaller effect as n grows and vice-versa.
is negative, we have a smaller effect as n grows and vice-versa.
It’s also interesting to look at  :
:
![E [ \textrm{time} | \textrm{gcd algorithm} ] = \alpha_0 + \alpha_1 n + \alpha_2 n^2 + \epsilon](https://s0.wp.com/latex.php?latex=E+%5B+%5Ctextrm%7Btime%7D+%7C+%5Ctextrm%7Bgcd+algorithm%7D+%5D+%3D++%5Calpha_0+%2B+%5Calpha_1+n+%2B+%5Calpha_2+n%5E2+%2B+%5Cepsilon+&bg=ffffff&fg=333333&s=2&c=20201002)
![E [ \textrm{time} | \textrm{mod algorithm} ] = (\alpha_0 + \alpha_3) + \alpha_1 n + \alpha_2 n^2 + \epsilon](https://s0.wp.com/latex.php?latex=E+%5B+%5Ctextrm%7Btime%7D+%7C+%5Ctextrm%7Bmod+algorithm%7D+%5D+%3D++%28%5Calpha_0+%2B+%5Calpha_3%29+%2B+%5Calpha_1+n+%2B+%5Calpha_2+n%5E2+%2B+%5Cepsilon+&bg=ffffff&fg=333333&s=2&c=20201002)
where ![E[\cdot]](https://s0.wp.com/latex.php?latex=E%5B%5Ccdot%5D&bg=ffffff&fg=333333&s=0&c=20201002) is the expected value. In this model, the effect of changing algorithms is supposed to be constant for any
is the expected value. In this model, the effect of changing algorithms is supposed to be constant for any  .
.
Let’s run this on GNU R:
model<-lm(time~n+I(n^2)+f, data=data)
summary(model)
This will give us
Call:
lm(formula = time ~ n + I(n^2) + f, data = data)
Residuals:
Min 1Q Median 3Q Max
-12.2097 -7.6267 -0.5312 7.7528 12.6358
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.190e+01 5.042e+00 2.361 0.0222 *
n -9.796e-04 3.860e-03 -0.254 0.8007
I(n^2) 3.618e-06 6.534e-07 5.537 1.14e-06 ***
f -2.265e+01 2.273e+00 -9.968 1.79e-13 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 8.35 on 50 degrees of freedom
Multiple R-Squared: 0.9386, Adjusted R-squared: 0.9349
F-statistic: 254.9 on 3 and 50 DF, p-value: < 2.2e-16
The estimate column holds the value for the 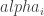 parameters defined on the equation above. The t value column is a measure of how far the parameter is from zero given its uncertainty. If the regression residuals follow a gaussian normal distribution, 1.96 (or -1.96) is a good critical value for considering the variable in question significant; in any case, values above 3 tend to indicate an important relationship.
parameters defined on the equation above. The t value column is a measure of how far the parameter is from zero given its uncertainty. If the regression residuals follow a gaussian normal distribution, 1.96 (or -1.96) is a good critical value for considering the variable in question significant; in any case, values above 3 tend to indicate an important relationship.
The effect of  is apparently zero, but
is apparently zero, but 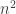 is significant and positive — which means the algorithm grows more-than-linearly on size. The effect of
is significant and positive — which means the algorithm grows more-than-linearly on size. The effect of  is very strongly negative, which indicates the second algorithm really tends to be faster.
is very strongly negative, which indicates the second algorithm really tends to be faster.
We can run, just for kicks, the same regression for memory usage. The algebraic analysis remains the same.
Call:
lm(formula = bytes ~ n + I(n^2) + f, data = data)
Residuals:
Min 1Q Median 3Q Max
-624215565 -421792810 -1493863 425410175 622244685
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.368e+08 2.753e+08 2.313 0.02485 *
n -2.654e+04 2.107e+05 -0.126 0.90027
I(n^2) 9.829e+01 3.567e+01 2.755 0.00816 **
f -1.250e+09 1.241e+08 -10.075 1.25e-13 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 455900000 on 50 degrees of freedom
Multiple R-Squared: 0.8419, Adjusted R-squared: 0.8324
F-statistic: 88.77 on 3 and 50 DF, p-value: < 2.2e-16
Compare the multiple 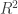 value between the two regressions. The
value between the two regressions. The 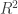 statistic measures how closely the model fits the data. One way to look at this is to affirm that apparently memory usage is also determined by something else we haven’t mentioned — this evidently being the size of the divisor list.
statistic measures how closely the model fits the data. One way to look at this is to affirm that apparently memory usage is also determined by something else we haven’t mentioned — this evidently being the size of the divisor list.
5. A better model
Let’s revise our equation.

We’ve added an additional “interaction” term. To see what this means, let’s look at expected values again:
![E [ \textrm{time} | \textrm{gcd algorithm} ] = \alpha_0 + \alpha_1 n + \alpha_2 n^2 + \epsilon](https://s0.wp.com/latex.php?latex=E+%5B+%5Ctextrm%7Btime%7D+%7C+%5Ctextrm%7Bgcd+algorithm%7D+%5D+%3D++%5Calpha_0+%2B+%5Calpha_1+n+%2B+%5Calpha_2+n%5E2+%2B+%5Cepsilon+&bg=ffffff&fg=333333&s=2&c=20201002)
![E [ \textrm{time} | \textrm{mod algorithm} ] = (\alpha_0 + \alpha_3) + (\alpha_1+\alpha_4) n + \alpha_2 n^2 + \epsilon](https://s0.wp.com/latex.php?latex=E+%5B+%5Ctextrm%7Btime%7D+%7C+%5Ctextrm%7Bmod+algorithm%7D+%5D+%3D++%28%5Calpha_0+%2B+%5Calpha_3%29+%2B+%28%5Calpha_1%2B%5Calpha_4%29+n+%2B+%5Calpha_2+n%5E2+%2B+%5Cepsilon+&bg=ffffff&fg=333333&s=2&c=20201002)
In this new model, the effect of changing algorithms is allowed to vary with the size of  as well. Let’s estimate this model:
as well. Let’s estimate this model:
Call:
lm(formula = time ~ n + I(n^2) + f + f:n, data = data)
Residuals:
Min 1Q Median 3Q Max
-4.56081 -1.30100 0.09815 1.67459 4.00706
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.622e+00 1.377e+00 -4.083 0.000164 ***
n 4.451e-03 9.600e-04 4.636 2.66e-05 ***
I(n^2) 3.618e-06 1.592e-07 22.723 < 2e-16 ***
f 1.240e+01 1.362e+00 9.100 4.19e-12 ***
n:f -1.086e-02 3.856e-04 -28.163 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.035 on 49 degrees of freedom
Multiple R-Squared: 0.9964, Adjusted R-squared: 0.9961
F-statistic: 3418 on 4 and 49 DF, p-value: < 2.2e-16
Now all the coefficients are indeed very significant, including the linear term on  . This gives us the following formulas for predicting the running time of both algorithms on a given
. This gives us the following formulas for predicting the running time of both algorithms on a given  :
:
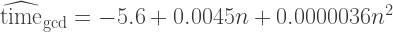
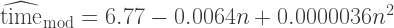
An interesting observation: the coefficient for  being positive means that the running time of the GCD algorithm starts lower; on the other hand, MOD will quickly outrun it (solve a simple inequality to find ranges of
being positive means that the running time of the GCD algorithm starts lower; on the other hand, MOD will quickly outrun it (solve a simple inequality to find ranges of  if you’re so inclined).
if you’re so inclined).
Conclusions
I might return to this topic if it arises enough interest. For the time being, I tried keeping it short and sweet, even if it meant glossing over all the relevant theoretical details. Discussion is appreciated, etc. etc. Oh, and remember this all was run on an old G4 mac mini, on the interpreter (not compiled/optimized), all while browsing and IMing at the same time. Don’t just benchmark this on JRuby on your dual Opteron and say your language leaves my language biting the dust.
]]>